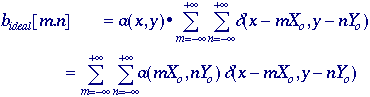Image Sampling

where X_o and Y_o are the sampling distances or intervals, d(*,*) is the ideal impulse function, and we have used eq. . (At some point, of course, the impulse function d(x,y) is converted to the discrete impulse function d[m,n].) Square sampling implies that X_o =Y_o. Sampling with an impulse function corresponds to sampling with an infinitesimally small point. 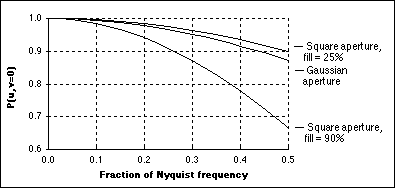This, however, does not correspond to the usual situation as illustrated in Figure 1. To take the effects of a finite sampling aperture p(x,y) into account, we can modify the sampling model as follows:

The combined effect of the aperture and sampling are best understood by examining the Fourier domain representation.

where _s = 2 /X_o is the sampling frequency in the x direction and _s = 2 /Y_o is the sampling frequency in the y direction. The aperture p(x,y) is frequently square, circular, or Gaussian with the associated P( , ). (See Table 4.) The periodic nature of the spectrum, described in eq. is clear from eq. .

 Sampling Density for Image Processing

To prevent the possible aliasing (overlapping) of spectral terms that is inherent in eq. two conditions must hold:

* Bandlimited A(u,v) -

* Nyquist sampling frequency -

where u_c and v_c are the cutoff frequencies in the x and y direction, respectively. Images that are acquired through lenses that are circularly-symmetric, aberration-free, and diffraction-limited will, in general, be bandlimited. The lens acts as a lowpass filter with a cutoff frequency in the frequency domain (eq. ) given by:

where NA is the numerical aperture of the lens and is the shortest wavelength of light used with the lens . If the lens does not meet one or more of these assumptions then it will still be bandlimited but at lower cutoff frequencies than those given in eq. . When working with the F-number (F) of the optics instead of the NA and in air (with index of refraction = 1.0), eq. becomes:

Sampling aperture

The aperture p(x,y) described above will have only a marginal effect on the final signal if the two conditions eqs. and are satisfied. Given, for example, the distance between samples X_o equals Y_o and a sampling aperture that is not wider than X_o, the effect on the overall spectrum--due to the A(u,v)P(u,v) behavior implied by eq.--is illustrated in Figure 16 for square and Gaussian apertures.

The spectra are evaluated along one axis of the 2D Fourier transform. The Gaussian aperture in Figure 16 has a width such that the sampling interval X_o contains +/-3 (99.7%) of the Gaussian. The rectangular apertures have a width such that one occupies 95% of the sampling interval and the other occupies 50% of the sampling interval. The 95% width translates to a fill factor of 90% and the 50% width to a fill factor of 25%. The fill factor is discussed in Section 7.5.2.

Figure 16: Aperture spectra P(u,v=0) for frequencies up to half the Nyquist frequency. For explanation of "fill" see text.

Sampling Density for Image Analysis

The "rules" for choosing the sampling density when the goal is image analysis--as opposed to image processing--are different. The fundamental difference is that the digitization of objects in an image into a collection of pixels introduces a form of spatial quantization noise that is not bandlimited. This leads to the following results for the choice of sampling density when one is interested in the measurement of area and (perimeter) length.

Sampling for area measurements

Assuming square sampling, X_o = Y_o and the unbiased algorithm for estimating area which involves simple pixel counting, the CV (see eq. ) of the area measurement is related to the sampling density by :

and in D dimensions:

where S is the number of samples per object diameter. In 2D the measurement is area, in 3D volume, and in D-dimensions hypervolume.

Sampling for length measurements

Again assuming square sampling and algorithms for estimating length based upon the Freeman chain-code representation (see Section 3.6.1), the CV of the length measurement is related to the sampling density per unit length as shown in Figure 17 (see .)

Figure 17: CV of length measurement for various algorithms.

The curves in Figure 17 were developed in the context of straight lines but similar results have been found for curves and closed contours. The specific formulas for length estimation use a chain code representation of a line and are based upon a linear combination of three numbers:

where N_e is the number of even chain codes, N_o the number of odd chain codes, and N_c the number of corners. The specific formulas are given in Table 7.

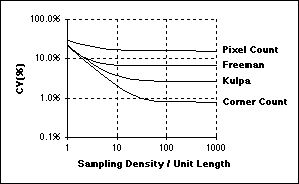
Table 7: Length estimation formulas based on chain code counts (N_e, N_o, N_c)

Conclusions on sampling

If one is interested in image processing, one should choose a sampling density based upon classical signal theory, that is, the Nyquist sampling theory. If one is interested in image analysis, one should choose a sampling density based upon the desired measurement accuracy (bias) and precision (CV). In a case of uncertainty, one should choose the higher of the two sampling densities (frequencies).